Tutoriel sur les transformations

Comme tous les packages graphiques, Matplotlib est construit sur un cadre de transformation pour se déplacer facilement entre les systèmes de coordonnées, le système de coordonnées des données utilisateur, le système de coordonnées des axes , le système de coordonnées de la figure et le système de coordonnées d'affichage . Dans 95 % de vos tracés, vous n'aurez pas besoin d'y penser, car cela se produit sous le capot, mais lorsque vous repoussez les limites de la génération de figures personnalisées, il est utile de comprendre ces objets afin de pouvoir réutiliser l'existant. transformations que Matplotlib met à votre disposition, ou créez les vôtres (voir matplotlib.transforms). Le tableau ci-dessous résume quelques systèmes de coordonnées utiles, une description de chaque système et l'objet de transformation pour passer de chaque système de coordonnées auafficher les coordonnées. Dans la colonne "Objet de transformation", axest une Axesinstance, figest une Figureinstance et subfigureest une SubFigureinstance.

Système de coordonnées	La description	Objet de transformation du système à l'affichage
"Les données"	Le système de coordonnées des données dans les Axes.	ax.transData
"haches"	Le système de coordonnées du Axes; (0, 0) est en bas à gauche des axes et (1, 1) est en haut à droite des axes.	ax.transAxes
"sous-figure"	Le système de coordonnées du SubFigure; (0, 0) est en bas à gauche de la sous-figure et (1, 1) est en haut à droite de la sous-figure. Si une figure n'a pas de sous-figures, c'est la même chose que transFigure.	subfigure.transSubfigure
"chiffre"	Le système de coordonnées du Figure; (0, 0) est en bas à gauche de la figure et (1, 1) est en haut à droite de la figure.	fig.transFigure
"figure-pouces"	Le système de coordonnées du Figureen pouces ; (0, 0) est en bas à gauche de la figure et (largeur, hauteur) est en haut à droite de la figure en pouces.	fig.dpi_scale_trans
"xaxis", "yaxis"	Systèmes de coordonnées mixtes, utilisant les coordonnées des données dans une direction et les coordonnées des axes dans l'autre.	ax.get_xaxis_transform(), ax.get_yaxis_transform()
"affichage"	Le système de coordonnées natif de la sortie ; (0, 0) est en bas à gauche de la fenêtre et (largeur, hauteur) est en haut à droite de la sortie en "unités d'affichage". L'interprétation exacte des unités dépend du back-end. Par exemple, il s'agit de pixels pour Agg et de points pour svg/pdf.	None, ou IdentityTransform()

Les Transformobjets sont naïfs aux systèmes de coordonnées source et de destination, mais les objets mentionnés dans le tableau ci-dessus sont construits pour prendre des entrées dans leur système de coordonnées et transformer l'entrée dans le système de coordonnées d' affichage . C'est pourquoi le système de coordonnées d'affichage a Nonepour la colonne "Objet de transformation" -- il est déjà dans les coordonnées d' affichage . Les conventions de dénomination et de destination sont une aide pour garder une trace des systèmes de coordonnées et des transformations "standard" disponibles.

Les transformations savent également comment s'inverser (via Transform.inverted) pour générer une transformation du système de coordonnées de sortie vers le système de coordonnées d'entrée. Par exemple, ax.transDataconvertit les valeurs des coordonnées de données en coordonnées d'affichage et ax.transData.inversed()est un matplotlib.transforms.Transformqui passe des coordonnées d'affichage aux coordonnées de données. Ceci est particulièrement utile lors du traitement d'événements à partir de l'interface utilisateur, qui se produisent généralement dans l'espace d'affichage, et que vous souhaitez savoir où le clic de souris ou l'appui sur la touche s'est produit dans votre système de coordonnées de données .

Notez que la spécification de la position des artistes dans les coordonnées d' affichage peut modifier leur emplacement relatif si la dpitaille ou de la figure change. Cela peut être source de confusion lors de l'impression ou de la modification de la résolution de l'écran, car l'objet peut changer d'emplacement et de taille. Par conséquent, il est plus courant que les artistes placés dans un Axe ou une figure aient leur transformation définie sur autre chose que le IdentityTransform(); la valeur par défaut lorsqu'un artiste est ajouté à un Axes en utilisant add_artistest que la transformation soit ax.transDataafin que vous puissiez travailler et penser en coordonnées de données et laisser Matplotlib s'occuper de la transformation à afficher .

Coordonnées des données

Commençons par la coordonnée la plus couramment utilisée, le système de coordonnées de données . Chaque fois que vous ajoutez des données aux axes, Matplotlib met à jour les limites de données, le plus souvent mises à jour avec les méthodes set_xlim()et . set_ylim()Par exemple, dans la figure ci-dessous, les limites de données s'étendent de 0 à 10 sur l'axe des x et de -1 à 1 sur l'axe des y.

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches

x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)

plt.show()

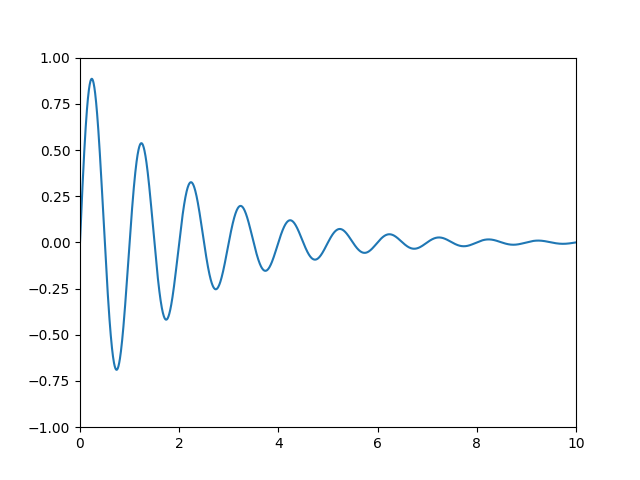
Vous pouvez utiliser l' ax.transDatainstance pour passer de vos données à votre système de coordonnées d' affichage , soit un point unique, soit une séquence de points, comme indiqué ci-dessous :

In [14]: type(ax.transData)
Out[14]: <class 'matplotlib.transforms.CompositeGenericTransform'>

In [15]: ax.transData.transform((5, 0))
Out[15]: array([ 335.175,  247.   ])

In [16]: ax.transData.transform([(5, 0), (1, 2)])
Out[16]:
array([[ 335.175,  247.   ],
       [ 132.435,  642.2  ]])

Vous pouvez utiliser la inverted() méthode pour créer une transformation qui vous mènera de l' affichage aux coordonnées de données :

In [41]: inv = ax.transData.inverted()

In [42]: type(inv)
Out[42]: <class 'matplotlib.transforms.CompositeGenericTransform'>

In [43]: inv.transform((335.175,  247.))
Out[43]: array([ 5.,  0.])

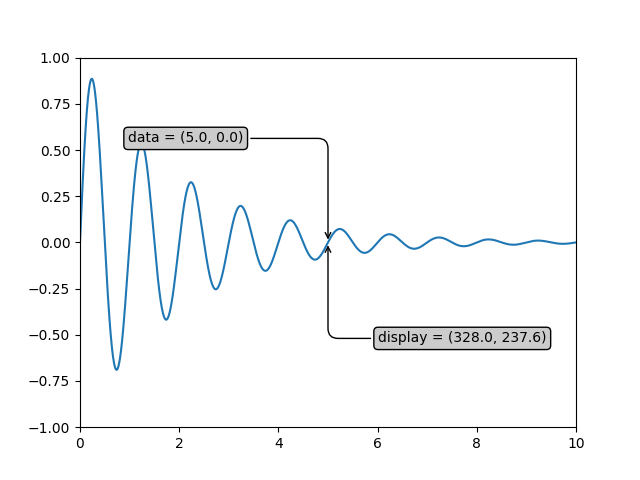
Si vous tapez avec ce didacticiel, les valeurs exactes des coordonnées d' affichage peuvent différer si vous avez une taille de fenêtre ou un paramètre dpi différent. De même, dans la figure ci-dessous, les points étiquetés affichés ne sont probablement pas les mêmes que dans la session ipython car les valeurs par défaut de la taille des figures de la documentation sont différentes.

x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)

xdata, ydata = 5, 0
# This computing the transform now, if anything
# (figure size, dpi, axes placement, data limits, scales..)
# changes re-calling transform will get a different value.
xdisplay, ydisplay = ax.transData.transform((xdata, ydata))

bbox = dict(boxstyle="round", fc="0.8")
arrowprops = dict(
    arrowstyle="->",
    connectionstyle="angle,angleA=0,angleB=90,rad=10")

offset = 72
ax.annotate('data = (%.1f, %.1f)' % (xdata, ydata),
            (xdata, ydata), xytext=(-2*offset, offset), textcoords='offset points',
            bbox=bbox, arrowprops=arrowprops)

disp = ax.annotate('display = (%.1f, %.1f)' % (xdisplay, ydisplay),
                   (xdisplay, ydisplay), xytext=(0.5*offset, -offset),
                   xycoords='figure pixels',
                   textcoords='offset points',
                   bbox=bbox, arrowprops=arrowprops)

plt.show()

Avertissement

Si vous exécutez le code source dans l'exemple ci-dessus dans un backend GUI, vous pouvez également constater que les deux flèches pour les données et les annotations d'affichage ne pointent pas exactement au même point. En effet, le point d'affichage a été calculé avant l'affichage de la figure et le backend de l'interface graphique peut légèrement redimensionner la figure lors de sa création. L'effet est plus prononcé si vous redimensionnez vous-même la figure. C'est une bonne raison pour laquelle vous souhaitez rarement travailler dans l'espace d' affichage , mais vous pouvez vous connecter au 'on_draw' Eventpour mettre à jour les coordonnées de la figure sur les dessins de la figure ; voir Gestion et sélection des événements .

Lorsque vous modifiez les limites x ou y de vos axes, les limites de données sont mises à jour afin que la transformation génère un nouveau point d'affichage. Notez que lorsque nous modifions simplement le ylim, seule la coordonnée d'affichage y est modifiée, et lorsque nous modifions également le xlim, les deux sont modifiés. Plus d'informations à ce sujet plus tard lorsque nous parlerons du Bbox.

In [54]: ax.transData.transform((5, 0))
Out[54]: array([ 335.175,  247.   ])

In [55]: ax.set_ylim(-1, 2)
Out[55]: (-1, 2)

In [56]: ax.transData.transform((5, 0))
Out[56]: array([ 335.175     ,  181.13333333])

In [57]: ax.set_xlim(10, 20)
Out[57]: (10, 20)

In [58]: ax.transData.transform((5, 0))
Out[58]: array([-171.675     ,  181.13333333])

Coordonnées des axes

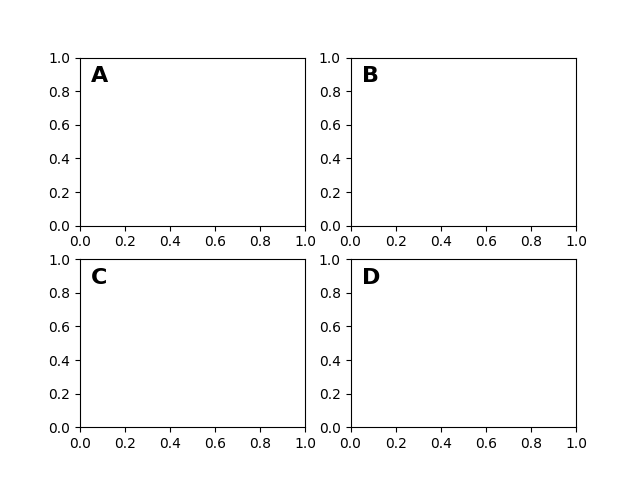
Après le système de coordonnées de données , les axes sont probablement le deuxième système de coordonnées le plus utile. Ici, le point (0, 0) est en bas à gauche de vos axes ou sous-parcelle, (0,5, 0,5) est le centre et (1,0, 1,0) est en haut à droite. Vous pouvez également faire référence à des points en dehors de la plage, donc (-0,1, 1,1) est à gauche et au-dessus de vos axes. Ce système de coordonnées est extrêmement utile lorsque vous placez du texte dans vos axes, car vous souhaitez souvent une bulle de texte à un emplacement fixe, par exemple, en haut à gauche du volet des axes, et que cet emplacement reste fixe lorsque vous effectuez un panoramique ou un zoom. Voici un exemple simple qui crée quatre panneaux et les étiquette 'A', 'B', 'C', 'D' comme vous le voyez souvent dans les revues.

fig = plt.figure()
for i, label in enumerate(('A', 'B', 'C', 'D')):
    ax = fig.add_subplot(2, 2, i+1)
    ax.text(0.05, 0.95, label, transform=ax.transAxes,
            fontsize=16, fontweight='bold', va='top')

plt.show()

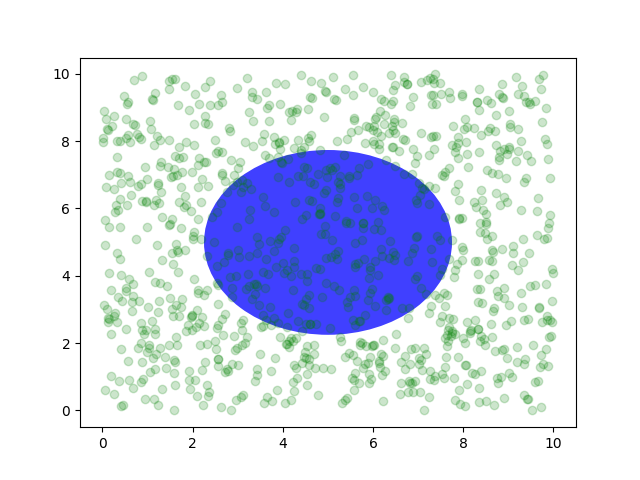
Vous pouvez également créer des lignes ou des patchs dans le système de coordonnées des axesax.transAxes , mais cela est moins utile d'après mon expérience que d'utiliser pour placer du texte. Néanmoins, voici un exemple idiot qui trace des points aléatoires dans l'espace de données et superpose un semi-transparent Circlecentré au milieu des axes avec un rayon d'un quart des axes - si vos axes ne conservent pas les proportions (voir set_aspect()) , cela ressemblera à une ellipse. Utilisez l'outil panoramique/zoom pour vous déplacer, ou modifiez manuellement les données xlim et ylim, et vous verrez les données se déplacer, mais le cercle restera fixe car il n'est pas dans les coordonnées des données et restera toujours au centre des axes .

fig, ax = plt.subplots()
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y, 'go', alpha=0.2)  # plot some data in data coordinates

circ = mpatches.Circle((0.5, 0.5), 0.25, transform=ax.transAxes,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

Transformations mixtes

Dessiner dans des espaces de coordonnées mixtes qui mélangent des axes avec des coordonnées de données est extrêmement utile, par exemple pour créer une étendue horizontale qui met en évidence une région des données y mais s'étend sur l'axe des x indépendamment des limites de données, du niveau de panoramique ou de zoom, etc. En fait, ces lignes et étendues mélangées sont si utiles que nous avons intégré des fonctions pour les rendre faciles à tracer (voir axhline(), axvline(), axhspan(), axvspan()) mais à des fins didactiques, nous implémenterons ici l'étendue horizontale en utilisant une transformation mélangée. Cette astuce ne fonctionne que pour les transformations séparables, comme vous le voyez dans les systèmes de coordonnées cartésiens normaux, mais pas sur les transformations inséparables comme le PolarTransform.

import matplotlib.transforms as transforms

fig, ax = plt.subplots()
x = np.random.randn(1000)

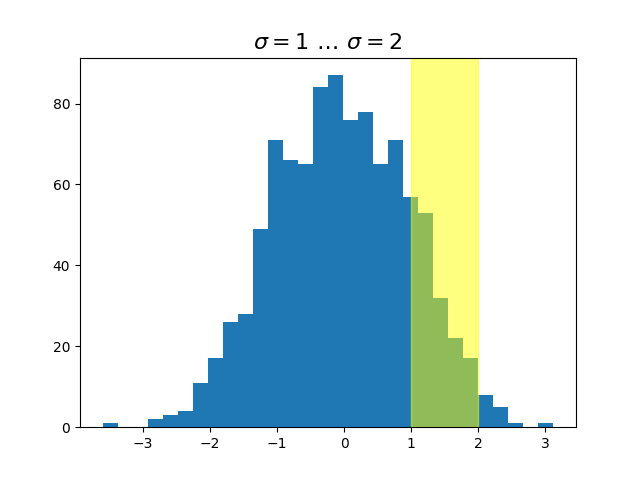
ax.hist(x, 30)
ax.set_title(r'$\sigma=1 \/ \dots \/ \sigma=2$', fontsize=16)

# the x coords of this transformation are data, and the y coord are axes
trans = transforms.blended_transform_factory(
    ax.transData, ax.transAxes)
# highlight the 1..2 stddev region with a span.
# We want x to be in data coordinates and y to span from 0..1 in axes coords.
rect = mpatches.Rectangle((1, 0), width=1, height=1, transform=trans,
                          color='yellow', alpha=0.5)
ax.add_patch(rect)

plt.show()

Noter

Les transformations mixtes où x est dans les coordonnées des données et y dans les coordonnées des axes sont si utiles que nous avons des méthodes d'assistance pour renvoyer les versions que Matplotlib utilise en interne pour dessiner des ticks, des ticklabels, etc. Les méthodes sont matplotlib.axes.Axes.get_xaxis_transform()et matplotlib.axes.Axes.get_yaxis_transform(). Ainsi dans l'exemple ci-dessus, l'appel à blended_transform_factory()peut être remplacé par get_xaxis_transform:

trans = ax.get_xaxis_transform()

Tracé en coordonnées physiques

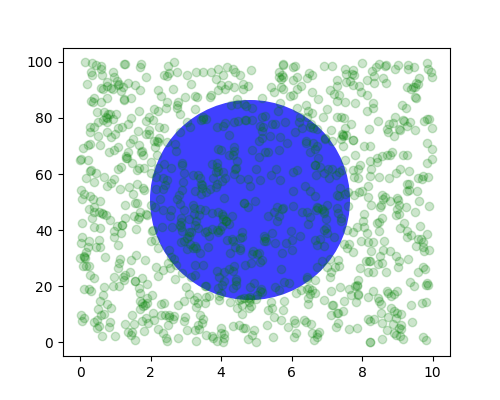
Parfois, nous voulons qu'un objet ait une certaine taille physique sur le tracé. Ici, nous dessinons le même cercle que ci-dessus, mais en coordonnées physiques. Si cela est fait de manière interactive, vous pouvez voir que la modification de la taille de la figure ne modifie pas le décalage du cercle par rapport au coin inférieur gauche, ne modifie pas sa taille et le cercle reste un cercle quel que soit le rapport d'aspect des axes.

fig, ax = plt.subplots(figsize=(5, 4))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2)  # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

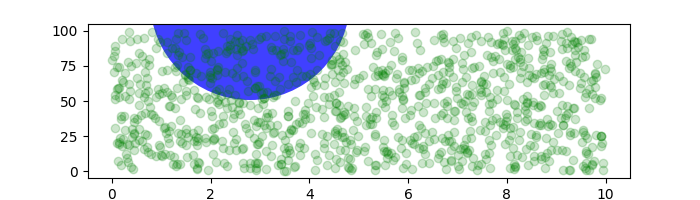
Si nous modifions la taille de la figure, le cercle ne change pas sa position absolue et est recadré.

fig, ax = plt.subplots(figsize=(7, 2))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2)  # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

Une autre utilisation consiste à placer un patch avec une dimension physique définie autour d'un point de données sur les axes. Ici, nous additionnons deux transformations. Le premier définit l'échelle de la taille de l'ellipse et le second définit sa position. L'ellipse est ensuite placée à l'origine, puis nous utilisons la transformation d'assistance ScaledTranslation pour la déplacer au bon endroit dans le ax.transDatasystème de coordonnées. Cet assistant est instancié avec :

trans = ScaledTranslation(xt, yt, scale_trans)

où xt et yt sont les décalages de translation, et scale_trans est une transformation qui met à l'échelle xt et yt au moment de la transformation avant d'appliquer les décalages.

Notez l'utilisation de l'opérateur plus sur les transformations ci-dessous. Ce code dit: appliquez d'abord la transformation d'échelle fig.dpi_scale_trans pour donner à l'ellipse la taille appropriée, mais toujours centrée sur (0, 0), puis traduisez les données vers xdata[0]et ydata[0]dans l'espace de données.

En utilisation interactive, l'ellipse garde la même taille même si les limites des axes sont modifiées via le zoom.

fig, ax = plt.subplots()
xdata, ydata = (0.2, 0.7), (0.5, 0.5)
ax.plot(xdata, ydata, "o")
ax.set_xlim((0, 1))

trans = (fig.dpi_scale_trans +
         transforms.ScaledTranslation(xdata[0], ydata[0], ax.transData))

# plot an ellipse around the point that is 150 x 130 points in diameter...
circle = mpatches.Ellipse((0, 0), 150/72, 130/72, angle=40,
                          fill=None, transform=trans)
ax.add_patch(circle)
plt.show()

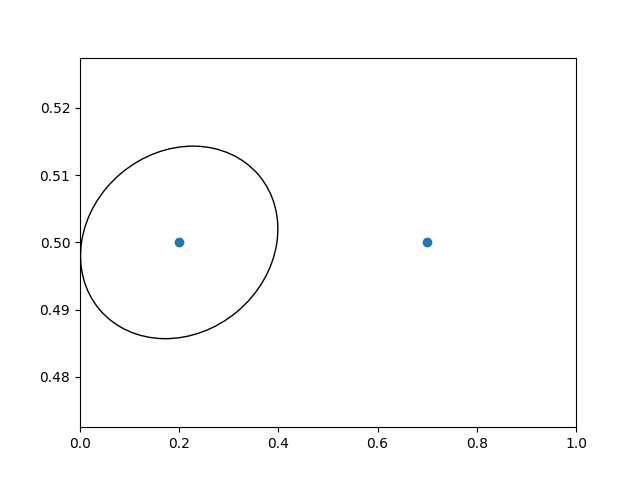
Noter

L'ordre de transformation est important. Ici, l'ellipse reçoit d' abord les bonnes dimensions dans l'espace d'affichage , puis est déplacée dans l'espace de données au bon endroit. Si nous avions fait le ScaledTranslationpremier, puis xdata[0]et ydata[0]seraient d'abord transformés pour afficher les coordonnées ( sur un moniteur de 200 dpi), puis ces coordonnées seraient mises à l'échelle en poussant le centre de l'ellipse loin de l'écran (c'est-à-dire ).[ 358.4  475.2]fig.dpi_scale_trans[ 71680.  95040.]

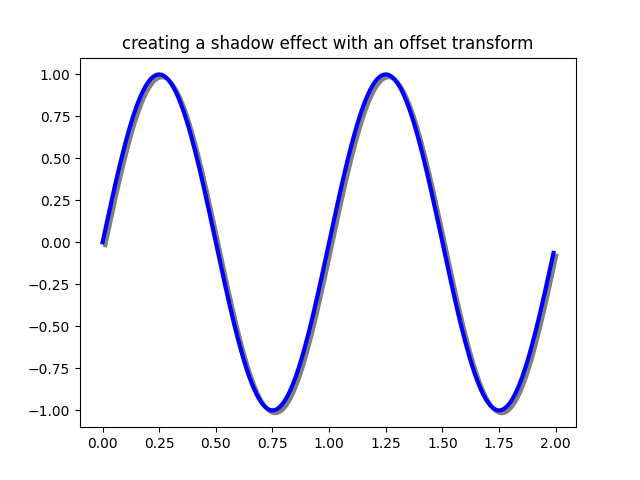
Utiliser des transformations de décalage pour créer un effet d'ombre

Une autre utilisation de ScaledTranslationest de créer une nouvelle transformation qui est décalée par rapport à une autre transformation, par exemple, pour placer un objet un peu décalé par rapport à un autre objet. En règle générale, vous souhaitez que le décalage soit dans une dimension physique, comme des points ou des pouces plutôt que dans des coordonnées de données , de sorte que l'effet de décalage soit constant à différents niveaux de zoom et paramètres de ppp.

Une utilisation pour un décalage est de créer un effet d'ombre, où vous dessinez un objet identique au premier juste à droite de celui-ci, et juste en dessous, en ajustant le zorder pour vous assurer que l'ombre est dessinée en premier, puis l'objet c'est ombre au-dessus.

Ici, nous appliquons les transformations dans l' ordre inverse de l'utilisation de ci- ScaledTranslationdessus. Le tracé est d'abord réalisé en coordonnées de données ( ax.transData) puis décalé de dxet dypoints à l'aide de fig.dpi_scale_trans. (En typographie, un point est de 1/72 pouces, et en spécifiant vos décalages en points, votre figure aura la même apparence quelle que soit la résolution dpi dans laquelle elle est enregistrée.)

fig, ax = plt.subplots()

# make a simple sine wave
x = np.arange(0., 2., 0.01)
y = np.sin(2*np.pi*x)
line, = ax.plot(x, y, lw=3, color='blue')

# shift the object over 2 points, and down 2 points
dx, dy = 2/72., -2/72.
offset = transforms.ScaledTranslation(dx, dy, fig.dpi_scale_trans)
shadow_transform = ax.transData + offset

# now plot the same data with our offset transform;
# use the zorder to make sure we are below the line
ax.plot(x, y, lw=3, color='gray',
        transform=shadow_transform,
        zorder=0.5*line.get_zorder())

ax.set_title('creating a shadow effect with an offset transform')
plt.show()

Noter

Le décalage en dpi et en pouces est un cas d'utilisation assez courant pour lequel nous avons une fonction d'assistance spéciale pour le créer dans matplotlib.transforms.offset_copy(), qui renvoie une nouvelle transformation avec un décalage supplémentaire. Donc ci-dessus on aurait pu faire :

shadow_transform = transforms.offset_copy(ax.transData,
         fig=fig, dx, dy, units='inches')

Le pipeline de transformation

La ax.transDatatransformation avec laquelle nous avons travaillé dans ce didacticiel est un composite de trois transformations différentes qui composent le pipeline de transformation de data -> display coordonnées. Michael Droettboom a implémenté le cadre de transformations, en prenant soin de fournir une API propre qui sépare les projections et les échelles non linéaires qui se produisent dans les tracés polaires et logarithmiques, des transformations affines linéaires qui se produisent lorsque vous effectuez un panoramique et un zoom. Il y a une efficacité ici, car vous pouvez effectuer un panoramique et un zoom sur vos axes, ce qui affecte la transformation affine, mais vous n'aurez peut-être pas besoin de calculer les échelles ou les projections non linéaires potentiellement coûteuses sur des événements de navigation simples. Il est également possible de multiplier ensemble des matrices de transformation affine, puis de les appliquer aux coordonnées en une seule étape. Ce n'est pas le cas de toutes les transformations possibles.

Voici comment l' ax.transDatainstance est définie dans la Axesclasse d'axe séparable de base :

self.transData = self.transScale + (self.transLimits + self.transAxes)

Nous avons été initiés à l' transAxesinstance ci-dessus dans Coordonnées des axes , qui mappe les coins (0, 0), (1, 1) des axes ou de la boîte englobante de la sous-parcelle pour afficher l'espace, alors regardons ces deux autres pièces.

self.transLimitsest la transformation qui vous emmène des données aux coordonnées des axes ; c'est-à-dire qu'il mappe votre vue xlim et ylim sur l'espace unitaire des axes ( transAxespuis prend cet espace unitaire pour afficher l'espace). Nous pouvons voir cela en action ici

In [80]: ax = plt.subplot()

In [81]: ax.set_xlim(0, 10)
Out[81]: (0, 10)

In [82]: ax.set_ylim(-1, 1)
Out[82]: (-1, 1)

In [84]: ax.transLimits.transform((0, -1))
Out[84]: array([ 0.,  0.])

In [85]: ax.transLimits.transform((10, -1))
Out[85]: array([ 1.,  0.])

In [86]: ax.transLimits.transform((10, 1))
Out[86]: array([ 1.,  1.])

In [87]: ax.transLimits.transform((5, 0))
Out[87]: array([ 0.5,  0.5])

et nous pouvons utiliser cette même transformation inversée pour revenir des coordonnées des axes unitaires aux coordonnées des données .

In [90]: inv.transform((0.25, 0.25))
Out[90]: array([ 2.5, -0.5])

Le dernier élément est l' self.transScaleattribut, qui est responsable de la mise à l'échelle non linéaire facultative des données, par exemple, pour les axes logarithmiques. Lorsqu'un Axes est initialement configuré, il est simplement défini sur la transformation d'identité, car les axes Matplotlib de base ont une échelle linéaire, mais lorsque vous appelez une fonction de mise à l'échelle logarithmique comme semilogx()ou définissez explicitement l'échelle sur logarithmique avec set_xscale(), alors l' ax.transScaleattribut est défini pour gérer la projection non linéaire. Les transformations d'échelles sont des propriétés des instances respectives xaxiset . yaxis AxisPar exemple, lorsque vous appelez ax.set_xscale('log'), l'axe des abscisses met à jour son échelle en une matplotlib.scale.LogScaleinstance.

Pour les axes non séparables les PolarAxes, il y a une autre pièce à considérer, la transformation de projection. Le transData matplotlib.projections.polar.PolarAxesest similaire à celui des axes matplotlib séparables typiques, avec une pièce supplémentaire transProjection :

self.transData = self.transScale + self.transProjection + \
    (self.transProjectionAffine + self.transAxes)

transProjectiongère la projection depuis l'espace, par exemple la latitude et la longitude pour les données cartographiques, ou le rayon et le thêta pour les données polaires, vers un système de coordonnées cartésien séparable. Il existe plusieurs exemples de projection dans le matplotlib.projectionspackage, et la meilleure façon d'en savoir plus est d'ouvrir la source de ces packages et de voir comment créer le vôtre, car Matplotlib prend en charge les axes et les projections extensibles. Michael Droettboom a fourni un bel exemple de tutoriel de création d'axes de projection Hammer ; voir Projection personnalisée .