Normalisation de la palette de couleurs

Les objets qui utilisent des palettes de couleurs par défaut mappent linéairement les couleurs dans la palette de couleurs des valeurs de données vmin à vmax . Par exemple:

pcm = ax.pcolormesh(x, y, Z, vmin=-1., vmax=1., cmap='RdBu_r')

mappera les données en Z linéairement de -1 à +1, donc Z=0 donnera une couleur au centre de la palette de couleurs RdBu_r (blanc dans ce cas).

Matplotlib effectue ce mappage en deux étapes, avec une normalisation des données d'entrée à [0, 1] se produisant en premier, puis un mappage sur les indices de la palette de couleurs. Les normalisations sont des classes définies dans le matplotlib.colors()module. La normalisation linéaire par défaut est matplotlib.colors.Normalize().

Les artistes qui associent les données à la couleur passent les arguments vmin et vmax pour construire une matplotlib.colors.Normalize()instance, puis l'appellent :

In [1]: import matplotlib as mpl

In [2]: norm = mpl.colors.Normalize(vmin=-1, vmax=1)

In [3]: norm(0)
Out[3]: 0.5

Cependant, il existe parfois des cas où il est utile de mapper des données sur des palettes de couleurs de manière non linéaire.

Logarithmique

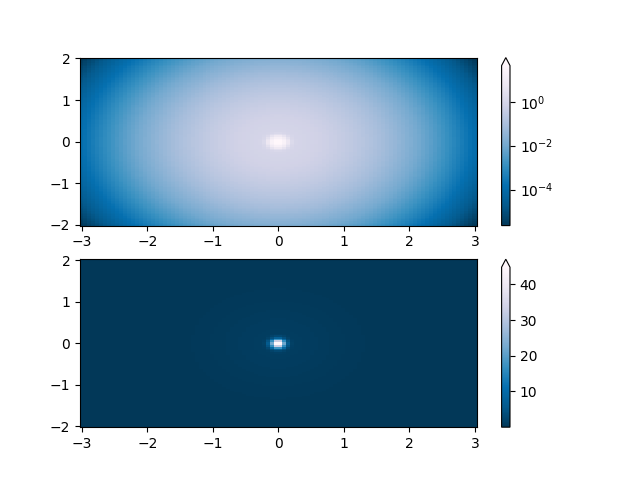
L'une des transformations les plus courantes consiste à tracer des données en prenant leur logarithme (en base 10). Cette transformation est utile pour afficher les modifications sur des échelles disparates. L'utilisation colors.LogNormnormalise les données via \(log_{10}\). Dans l'exemple ci-dessous, il y a deux bosses, l'une beaucoup plus petite que l'autre. En utilisant colors.LogNorm, la forme et l'emplacement de chaque bosse peuvent être clairement vus :

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import matplotlib.cbook as cbook
from matplotlib import cm

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]

# A low hump with a spike coming out of the top right.  Needs to have
# z/colour axis on a log scale so we see both hump and spike.  linear
# scale only shows the spike.
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X * 10)**2 - (Y * 10)**2)
Z = Z1 + 50 * Z2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolor(X, Y, Z,
                   norm=colors.LogNorm(vmin=Z.min(), vmax=Z.max()),
                   cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')

pcm = ax[1].pcolor(X, Y, Z, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
plt.show()

Centré

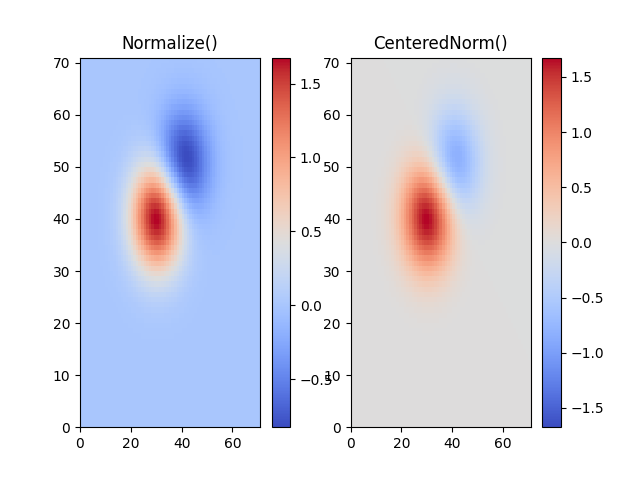
Dans de nombreux cas, les données sont symétriques autour d'un centre, par exemple, des anomalies positives et négatives autour d'un centre 0. Dans ce cas, nous aimerions que le centre soit mappé à 0,5 et que le point de données avec le plus grand écart par rapport au centre soit mappé à 1,0, si sa valeur est supérieure au centre, ou à 0,0 dans le cas contraire. La norme colors.CenteredNormcrée automatiquement un tel mappage. Il est bien adapté pour être combiné avec une palette de couleurs divergente qui utilise des bords de couleurs différentes qui se rejoignent au centre à une couleur non saturée.

Si le centre de symétrie est différent de 0, il peut être défini avec l' argument vcenter . Pour une mise à l'échelle logarithmique des deux côtés du centre, voir ci- colors.SymLogNormdessous ; pour appliquer un mappage différent au-dessus et au-dessous du centre, utilisez colors.TwoSlopeNormci-dessous.

delta = 0.1
x = np.arange(-3.0, 4.001, delta)
y = np.arange(-4.0, 3.001, delta)
X, Y = np.meshgrid(x, y)
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (0.9*Z1 - 0.5*Z2) * 2

# select a divergent colormap
cmap = cm.coolwarm

fig, (ax1, ax2) = plt.subplots(ncols=2)
pc = ax1.pcolormesh(Z, cmap=cmap)
fig.colorbar(pc, ax=ax1)
ax1.set_title('Normalize()')

pc = ax2.pcolormesh(Z, norm=colors.CenteredNorm(), cmap=cmap)
fig.colorbar(pc, ax=ax2)
ax2.set_title('CenteredNorm()')

plt.show()

Logarithmique symétrique

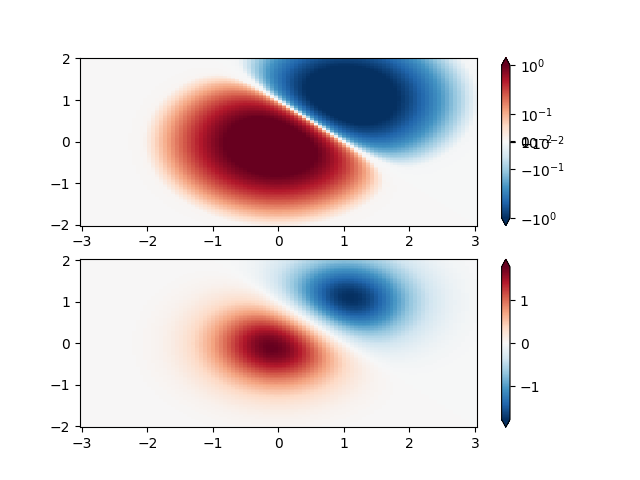
De même, il arrive parfois qu'il y ait des données positives et négatives, mais on aimerait quand même une mise à l'échelle logarithmique appliquée aux deux. Dans ce cas, les nombres négatifs sont également mis à l'échelle de manière logarithmique et mappés sur des nombres plus petits ; par exemple, si vmin=-vmax, alors les nombres négatifs sont mappés de 0 à 0,5 et les positifs de 0,5 à 1.

Étant donné que le logarithme des valeurs proches de zéro tend vers l'infini, une petite plage autour de zéro doit être cartographiée linéairement. Le paramètre linthresh permet à l'utilisateur de spécifier la taille de cette plage (- linthresh , linthresh ). La taille de cette plage dans la palette de couleurs est définie par linscale . Lorsque linscale == 1.0 (valeur par défaut), l'espace utilisé pour les moitiés positive et négative de la plage linéaire sera égal à une décade dans la plage logarithmique.

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (Z1 - Z2) * 2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolormesh(X, Y, Z,
                       norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
                                              vmin=-1.0, vmax=1.0, base=10),
                       cmap='RdBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='both')

pcm = ax[1].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z), shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='both')
plt.show()

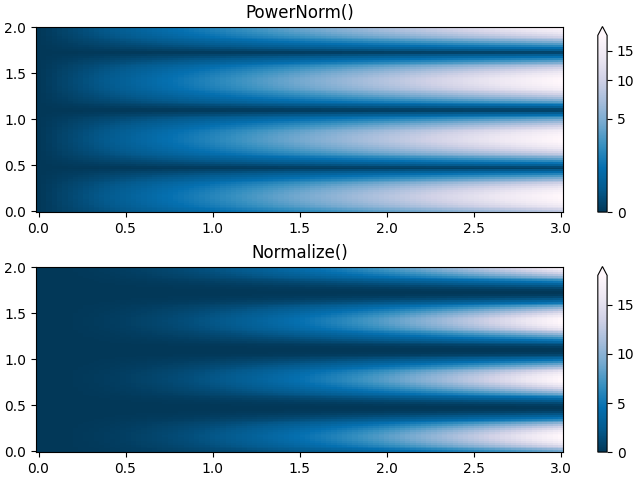
Loi de puissance

Parfois, il est utile de remapper les couleurs sur une relation de loi de puissance (c'est-à-dire\(y=x^{\gamma}\), où\(\gamma\)est la puissance). Pour cela nous utilisons le colors.PowerNorm. Il prend comme argument gamma ( gamma == 1.0 donnera juste la normalisation linéaire par défaut):

Noter

Il devrait probablement y avoir une bonne raison pour tracer les données en utilisant ce type de transformation. Les visualiseurs techniques sont habitués aux axes linéaires et logarithmiques et aux transformations de données. Les lois de puissance sont moins courantes et les téléspectateurs doivent être explicitement informés qu'elles ont été utilisées.

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2

fig, ax = plt.subplots(2, 1, constrained_layout=True)

pcm = ax[0].pcolormesh(X, Y, Z1, norm=colors.PowerNorm(gamma=0.5),
                       cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')
ax[0].set_title('PowerNorm()')

pcm = ax[1].pcolormesh(X, Y, Z1, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
ax[1].set_title('Normalize()')
plt.show()

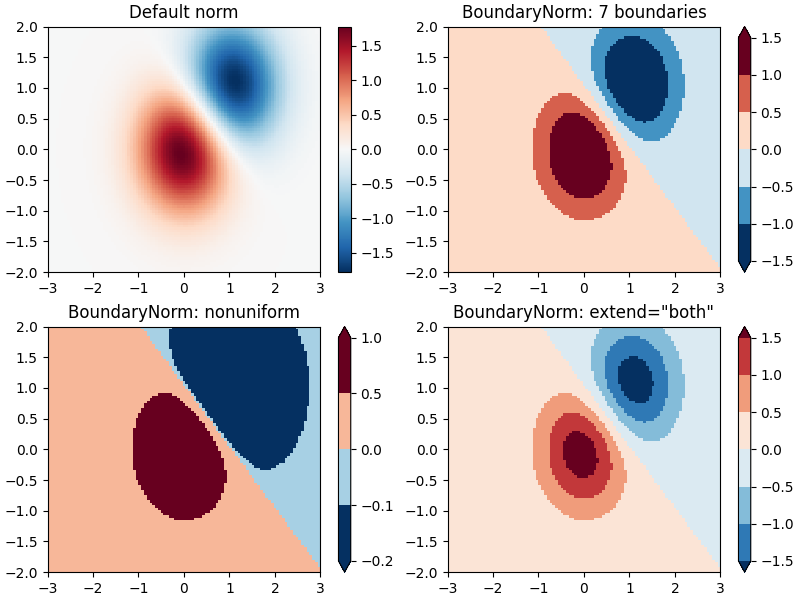
Bornes discrètes

Une autre normalisation fournie avec Matplotlib est colors.BoundaryNorm. En plus de vmin et vmax , cela prend comme arguments les limites entre lesquelles les données doivent être mappées. Les couleurs sont alors réparties linéairement entre ces « bornes ». Il peut également prendre un argument extend pour ajouter des valeurs supérieures et/ou inférieures hors limites à la plage sur laquelle les couleurs sont distribuées. Par exemple:

In [4]: import matplotlib.colors as colors

In [5]: bounds = np.array([-0.25, -0.125, 0, 0.5, 1])

In [6]: norm = colors.BoundaryNorm(boundaries=bounds, ncolors=4)

In [7]: print(norm([-0.2, -0.15, -0.02, 0.3, 0.8, 0.99]))
[0 0 1 2 3 3]

Remarque : Contrairement aux autres normes, cette norme renvoie des valeurs de 0 à ncolors -1.

N = 100
X, Y = np.meshgrid(np.linspace(-3, 3, N), np.linspace(-2, 2, N))
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = ((Z1 - Z2) * 2)[:-1, :-1]

fig, ax = plt.subplots(2, 2, figsize=(8, 6), constrained_layout=True)
ax = ax.flatten()

# Default norm:
pcm = ax[0].pcolormesh(X, Y, Z, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[0], orientation='vertical')
ax[0].set_title('Default norm')

# Even bounds give a contour-like effect:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
ax[1].set_title('BoundaryNorm: 7 boundaries')

# Bounds may be unevenly spaced:
bounds = np.array([-0.2, -0.1, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[2].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
ax[2].set_title('BoundaryNorm: nonuniform')

# With out-of-bounds colors:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256, extend='both')
pcm = ax[3].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
# The colorbar inherits the "extend" argument from BoundaryNorm.
fig.colorbar(pcm, ax=ax[3], orientation='vertical')
ax[3].set_title('BoundaryNorm: extend="both"')
plt.show()

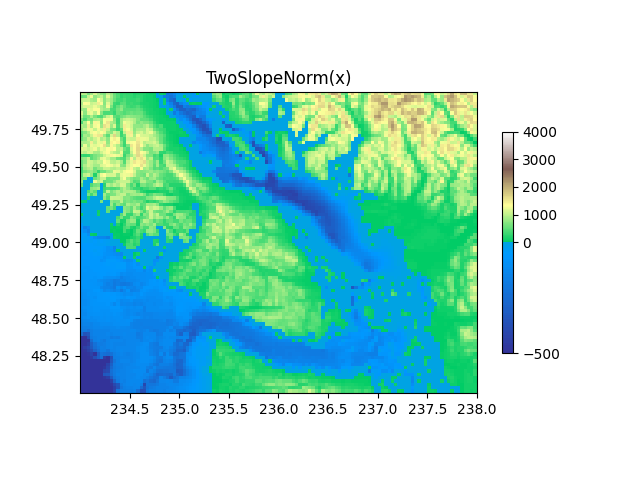
TwoSlopeNorm : Cartographie différente de chaque côté d'un centre

Parfois, nous voulons avoir une palette de couleurs différente de chaque côté d'un point central conceptuel, et nous voulons que ces deux palettes de couleurs aient des échelles linéaires différentes. Un exemple est une carte topographique où la terre et l'océan ont un centre à zéro, mais la terre a généralement une plage d'altitude plus grande que l'eau a une plage de profondeur, et ils sont souvent représentés par une palette de couleurs différente.

dem = cbook.get_sample_data('topobathy.npz', np_load=True)
topo = dem['topo']
longitude = dem['longitude']
latitude = dem['latitude']

fig, ax = plt.subplots()
# make a colormap that has land and ocean clearly delineated and of the
# same length (256 + 256)
colors_undersea = plt.cm.terrain(np.linspace(0, 0.17, 256))
colors_land = plt.cm.terrain(np.linspace(0.25, 1, 256))
all_colors = np.vstack((colors_undersea, colors_land))
terrain_map = colors.LinearSegmentedColormap.from_list(
    'terrain_map', all_colors)

# make the norm:  Note the center is offset so that the land has more
# dynamic range:
divnorm = colors.TwoSlopeNorm(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=divnorm,
                    cmap=terrain_map, shading='auto')
# Simple geographic plot, set aspect ratio because distance between lines of
# longitude depends on latitude.
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('TwoSlopeNorm(x)')
cb = fig.colorbar(pcm, shrink=0.6)
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])
plt.show()

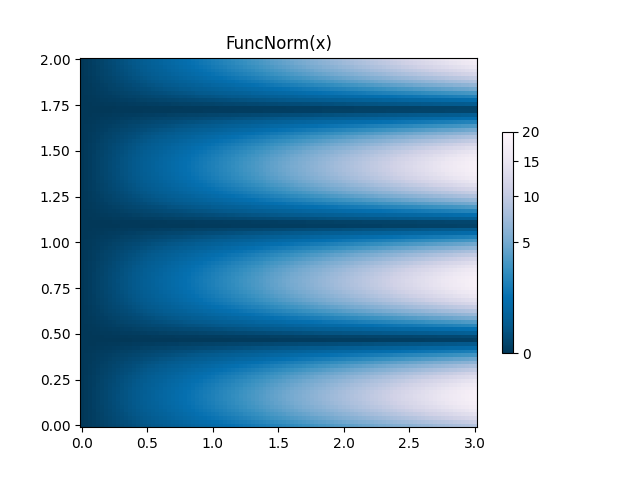
FuncNorm : normalisation de fonctions arbitraires

Si les normes ci-dessus ne fournissent pas la normalisation souhaitée, vous pouvez les utiliser FuncNormpour définir les vôtres. Notez que cet exemple est le même PowerNormqu'avec une puissance de 0,5 :

def _forward(x):
    return np.sqrt(x)


def _inverse(x):
    return x**2

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots()

norm = colors.FuncNorm((_forward, _inverse), vmin=0, vmax=20)
pcm = ax.pcolormesh(X, Y, Z1, norm=norm, cmap='PuBu_r', shading='auto')
ax.set_title('FuncNorm(x)')
fig.colorbar(pcm, shrink=0.6)
plt.show()

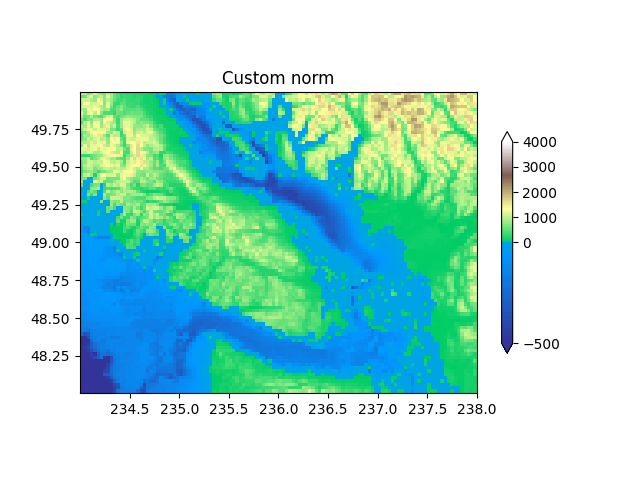
Normalisation personnalisée : implémentez manuellement deux plages linéaires

Ce TwoSlopeNormqui précède est un exemple utile pour définir votre propre norme. Remarque pour que la barre de couleurs fonctionne, vous devez définir un inverse pour votre norme :

class MidpointNormalize(colors.Normalize):
    def __init__(self, vmin=None, vmax=None, vcenter=None, clip=False):
        self.vcenter = vcenter
        super().__init__(vmin, vmax, clip)

    def __call__(self, value, clip=None):
        # I'm ignoring masked values and all kinds of edge cases to make a
        # simple example...
        # Note also that we must extrapolate beyond vmin/vmax
        x, y = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1.]
        return np.ma.masked_array(np.interp(value, x, y,
                                            left=-np.inf, right=np.inf))

    def inverse(self, value):
        y, x = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1]
        return np.interp(value, x, y, left=-np.inf, right=np.inf)


fig, ax = plt.subplots()
midnorm = MidpointNormalize(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=midnorm,
                    cmap=terrain_map, shading='auto')
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('Custom norm')
cb = fig.colorbar(pcm, shrink=0.6, extend='both')
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])

plt.show()