matplotlib.axes.Axes.csd

Haches. csd ( x , y , NFFT = Aucun , Fs = Aucun , Fc = Aucun , detrend = Aucun , window = Aucun , noverlap = Aucun , pad_to = Aucun , côtés = Aucun , scale_by_freq = Aucun , return_line = Aucun , * , data = Aucun ,** kwargs )

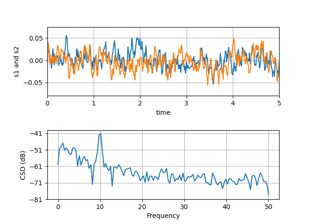
Tracez la densité spectrale croisée.

La densité spectrale croisée\(P_{xy}\)par la méthode du périodogramme moyen de Welch. Les vecteurs x et y sont divisés en segments de longueur NFFT . Chaque segment est redressé par la fonction detrend et fenêtré par la fonction window . noverlap donne la longueur du chevauchement entre les segments. Le produit des FFT directes de x et y est moyenné sur chaque segment pour calculer\(P_{xy}\), avec une mise à l'échelle pour corriger la perte de puissance due au fenêtrage.

Si len( x ) < NFFT ou len( y ) < NFFT , ils seront remplis de zéros à NFFT .

Paramètres :

x, y tableaux ou séquences 1-D

Tableaux ou séquences contenant les données.

Fs flottant, par défaut : 2

La fréquence d'échantillonnage (échantillons par unité de temps). Il est utilisé pour calculer les fréquences de Fourier, freqs , en cycles par unité de temps.

window callable ou ndarray, par défaut :window_hanning

Une fonction ou un vecteur de longueur NFFT . Pour créer des vecteurs de fenêtre, voir window_hanning, window_none, numpy.blackman, numpy.hamming, numpy.bartlett, scipy.signal, scipy.signal.get_window, etc. Si une fonction est passée en argument, elle doit prendre un segment de données en argument et renvoyer la version fenêtrée du segment.

côtés {'default', 'unilatéral', 'bilatéral'}, facultatif

Quels côtés du spectre revenir. 'default' est unilatéral pour les données réelles et bilatéral pour les données complexes. 'unilatéral' force le retour d'un spectre unilatéral, tandis que 'bilatéral' force bilatéral.

pad_to entier , facultatif

Le nombre de points auxquels le segment de données est complété lors de l'exécution de la FFT. Cela peut être différent de NFFT , qui spécifie le nombre de points de données utilisés. Sans augmenter la résolution réelle du spectre (la distance minimale entre les pics résolubles), cela peut donner plus de points dans le tracé, permettant plus de détails. Cela correspond au paramètre nfft dans l'appel à . La valeur par défaut est None, ce qui définit pad_to égal à NFFT

NFFT entier , par défaut : 256

Le nombre de points de données utilisés dans chaque bloc pour la FFT. Une puissance 2 est la plus efficace. Cela ne doit PAS être utilisé pour obtenir un remplissage à zéro, sinon la mise à l'échelle du résultat sera incorrecte ; utilisez pad_to pour cela à la place.

detrend {'none', 'mean', 'linear'} ou appelable, par défaut : 'none'

La fonction appliquée à chaque segment avant fft-ing, conçue pour supprimer la tendance moyenne ou linéaire. Contrairement à MATLAB, où le paramètre detrend est un vecteur, dans Matplotlib, il s'agit d'une fonction. Le mlab module définit detrend_none, detrend_meanet detrend_linear, mais vous pouvez également utiliser une fonction personnalisée. Vous pouvez également utiliser une chaîne pour choisir l'une des fonctions : 'none' calls detrend_none. appels "méchants" detrend_mean. appels "linéaires" detrend_linear.

scale_by_freq booléen , par défaut : Vrai

Indique si les valeurs de densité résultantes doivent être mises à l'échelle par la fréquence de mise à l'échelle, qui donne la densité en unités de 1/Hz. Cela permet une intégration sur les valeurs de fréquence renvoyées. La valeur par défaut est True pour la compatibilité MATLAB.

noverlap int, par défaut : 0 (pas de chevauchement)

Le nombre de points de chevauchement entre les segments.

Fc entier, par défaut : 0

La fréquence centrale de x , qui compense les étendues x du tracé pour refléter la plage de fréquences utilisée lorsqu'un signal est acquis, puis filtré et sous-échantillonné en bande de base.

return_line bool, par défaut : False

Indique s'il faut inclure l'objet ligne tracé dans les valeurs renvoyées.

Retours :

Tableau Pxy 1-D

Les valeurs du spectre croisé\(P_{xy}\)avant mise à l'échelle (valeur complexe).

freqs tableau 1-D

Les fréquences correspondant aux éléments de Pxy .

ligneLine2D

La ligne créée par cette fonction. Renvoyé uniquement si return_line est True.

Autres paramètres :

objet de données indexable, facultatif

S'ils sont fournis, les paramètres suivants acceptent également une chaîne s, qui est interprétée comme data[s](sauf si cela déclenche une exception) :

x , y

**kwargs

Les arguments de mot-clé contrôlent les Line2Dpropriétés :

Propriété	La description
agg_filter	une fonction de filtre, qui prend un tableau flottant (m, n, 3) et une valeur dpi, et renvoie un tableau (m, n, 3) et deux décalages à partir du coin inférieur gauche de l'image
alpha	scalaire ou Aucun
animated	bourdonner
antialiasedou aa	bourdonner
clip_box	Bbox
clip_on	bourdonner
clip_path	Patch ou (chemin, transformation) ou aucun
colorou c	Couleur
dash_capstyle	CapStyleou {'bout', 'en saillie', 'rond'}
dash_joinstyle	JoinStyleou {'onglet', 'rond', 'biseau'}
dashes	séquence de flottants (on/off encre en points) ou (Aucun, Aucun)
data	(2, N) tableau ou deux tableaux 1D
drawstyleou dès	{'default', 'steps', 'steps-pre', 'steps-mid', 'steps-post'}, par défaut : 'default'
figure	Figure
fillstyle	{'plein', 'gauche', 'droite', 'bas', 'haut', 'aucun'}
gapcolor	couleur ou Aucun
gid	chaîne
in_layout	bourdonner
label	objet
linestyleou ls	{'-', '--', '-.', ':', '', (décalage, on-off-seq), ...}
linewidthou lw	flotteur
marker	chaîne de style marqueur, PathouMarkerStyle
markeredgecolorou mec	Couleur
markeredgewidthou miauler	flotteur
markerfacecolorou mfc	Couleur
markerfacecoloraltou mfcalt	Couleur
markersizeou ms	flotteur
markevery	None ou int ou (int, int) ou slice ou list[int] ou float ou (float, float) ou list[bool]
mouseover	bourdonner
path_effects	AbstractPathEffect
picker	float ou callable[[Artist, Event], tuple[bool, dict]]
pickradius	inconnue
rasterized	bourdonner
sketch_params	(échelle : flottant, longueur : flottant, caractère aléatoire : flottant)
snap	booléen ou Aucun
solid_capstyle	CapStyleou {'bout', 'en saillie', 'rond'}
solid_joinstyle	JoinStyleou {'onglet', 'rond', 'biseau'}
transform	inconnue
url	chaîne
visible	bourdonner
xdata	Tableau 1D
ydata	Tableau 1D
zorder	flotteur

Voir également

psd

équivaut à définir .y = x

Remarques

Pour le traçage, la puissance est tracée comme \(10 \log_{10}(P_{xy})\)pour les décibels, cependant\(P_{xy}\)lui-même est retourné.

Références

Bendat & Piersol -- Données aléatoires : Procédures d'analyse et de mesure, John Wiley & Sons (1986)

Exemples utilisant matplotlib.axes.Axes.csd

Démo CSD

Démo CSD