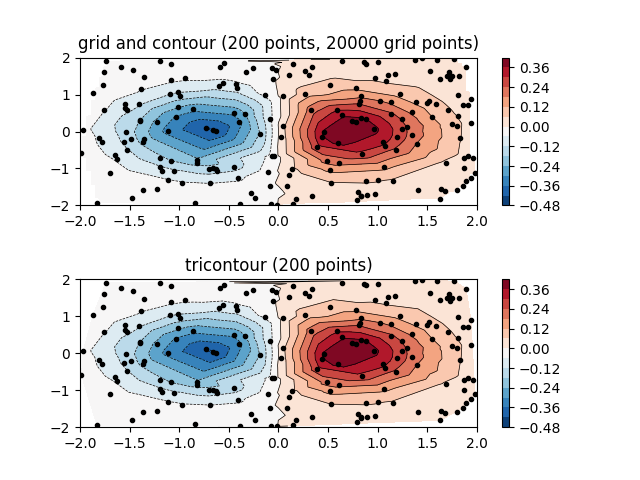
Tracé de contour de données irrégulièrement espacées #

Comparaison d'un tracé de contour de données irrégulièrement espacées interpolées sur une grille régulière par rapport à un tracé tricontour pour une grille triangulaire non structurée.

Comme contouret contourfs'attendent à ce que les données vivent sur une grille régulière, tracer un tracé de contour de données espacées de manière irrégulière nécessite différentes méthodes. Les deux options sont :

Interpolez d'abord les données sur une grille régulière. Cela peut être fait avec des moyens embarqués, par exemple via LinearTriInterpolatorou en utilisant une fonctionnalité externe, par exemple via scipy.interpolate.griddata. Ensuite, tracez les données interpolées avec l'habituel contour.
Utilisez directement tricontourou tricontourfqui effectuera une triangulation en interne.

Cet exemple montre les deux méthodes en action.

import matplotlib.pyplot as plt
import matplotlib.tri as tri
import numpy as np

np.random.seed(19680801)
npts = 200
ngridx = 100
ngridy = 200
x = np.random.uniform(-2, 2, npts)
y = np.random.uniform(-2, 2, npts)
z = x * np.exp(-x**2 - y**2)

fig, (ax1, ax2) = plt.subplots(nrows=2)

# -----------------------
# Interpolation on a grid
# -----------------------
# A contour plot of irregularly spaced data coordinates
# via interpolation on a grid.

# Create grid values first.
xi = np.linspace(-2.1, 2.1, ngridx)
yi = np.linspace(-2.1, 2.1, ngridy)

# Linearly interpolate the data (x, y) on a grid defined by (xi, yi).
triang = tri.Triangulation(x, y)
interpolator = tri.LinearTriInterpolator(triang, z)
Xi, Yi = np.meshgrid(xi, yi)
zi = interpolator(Xi, Yi)

# Note that scipy.interpolate provides means to interpolate data on a grid
# as well. The following would be an alternative to the four lines above:
# from scipy.interpolate import griddata
# zi = griddata((x, y), z, (xi[None, :], yi[:, None]), method='linear')

ax1.contour(xi, yi, zi, levels=14, linewidths=0.5, colors='k')
cntr1 = ax1.contourf(xi, yi, zi, levels=14, cmap="RdBu_r")

fig.colorbar(cntr1, ax=ax1)
ax1.plot(x, y, 'ko', ms=3)
ax1.set(xlim=(-2, 2), ylim=(-2, 2))
ax1.set_title('grid and contour (%d points, %d grid points)' %
              (npts, ngridx * ngridy))

# ----------
# Tricontour
# ----------
# Directly supply the unordered, irregularly spaced coordinates
# to tricontour.

ax2.tricontour(x, y, z, levels=14, linewidths=0.5, colors='k')
cntr2 = ax2.tricontourf(x, y, z, levels=14, cmap="RdBu_r")

fig.colorbar(cntr2, ax=ax2)
ax2.plot(x, y, 'ko', ms=3)
ax2.set(xlim=(-2, 2), ylim=(-2, 2))
ax2.set_title('tricontour (%d points)' % npts)

plt.subplots_adjust(hspace=0.5)
plt.show()

grille et contour (200 points, 20000 points de grille), tricontour (200 points)

Références

L'utilisation des fonctions, méthodes, classes et modules suivants est illustrée dans cet exemple :

Galerie générée par Sphinx-Gallery