Types de projection de tracé 3D

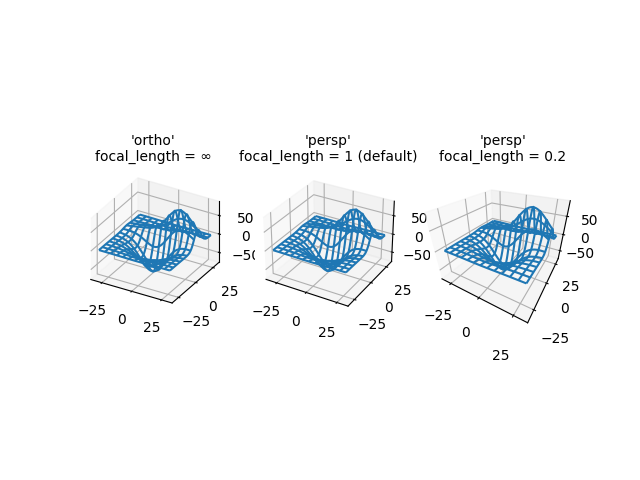
Illustre les différentes projections de caméra pour les tracés 3D et les effets de la modification de la distance focale pour une projection en perspective. Notez que Matplotlib corrige l'effet "zoom" de la modification de la distance focale.

La distance focale par défaut de 1 correspond à un champ de vision (FOV) de 90 degrés. Une focale augmentée entre 1 et l'infini "aplatit" l'image, tandis qu'une focale diminuée entre 1 et 0 exagère la perspective et donne à l'image plus de profondeur apparente. A la limite, une distance focale de l'infini correspond à une projection orthogonale après correction de l'effet de zoom.

Vous pouvez calculer la distance focale à partir d'un FOV via l'équation :

\[1 / \tan (\mathrm{FOV} / 2)\]

Ou vice versa:

\[\mathrm{FOV} = 2 \arctan (1 / \mathrm{focal length})\]

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt


fig, axs = plt.subplots(1, 3, subplot_kw={'projection': '3d'})

# Get the test data
X, Y, Z = axes3d.get_test_data(0.05)

# Plot the data
for ax in axs:
    ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)

# Set the orthographic projection.
axs[0].set_proj_type('ortho')  # FOV = 0 deg
axs[0].set_title("'ortho'\nfocal_length = ∞", fontsize=10)

# Set the perspective projections
axs[1].set_proj_type('persp')  # FOV = 90 deg
axs[1].set_title("'persp'\nfocal_length = 1 (default)", fontsize=10)

axs[2].set_proj_type('persp', focal_length=0.2)  # FOV = 157.4 deg
axs[2].set_title("'persp'\nfocal_length = 0.2", fontsize=10)

plt.show()