Remplir entre et Alpha

La fill_betweenfonction génère une région ombrée entre une limite min et max qui est utile pour illustrer les plages. Il a un argument très pratique wherepour combiner le remplissage avec des plages logiques, par exemple, pour simplement remplir une courbe au-dessus d'une certaine valeur de seuil.

À son niveau le plus élémentaire, fill_betweenpeut être utilisé pour améliorer l'apparence visuelle d'un graphique. Comparons deux graphiques de données financières avec un simple tracé linéaire à gauche et une ligne pleine à droite.

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.cbook as cbook


# load up some sample financial data
r = (cbook.get_sample_data('goog.npz', np_load=True)['price_data']
     .view(np.recarray))
# create two subplots with the shared x and y axes
fig, (ax1, ax2) = plt.subplots(1, 2, sharex=True, sharey=True)

pricemin = r.close.min()

ax1.plot(r.date, r.close, lw=2)
ax2.fill_between(r.date, pricemin, r.close, alpha=0.7)

for ax in ax1, ax2:
    ax.grid(True)
    ax.label_outer()

ax1.set_ylabel('price')

fig.suptitle('Google (GOOG) daily closing price')
fig.autofmt_xdate()

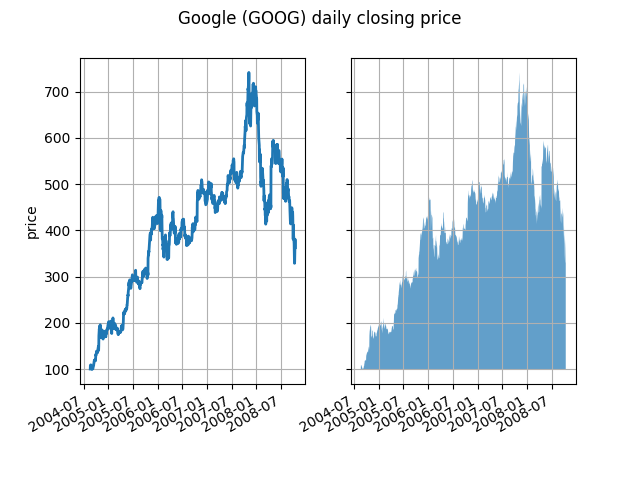
Le canal alpha n'est pas nécessaire ici, mais il peut être utilisé pour adoucir les couleurs pour des tracés plus attrayants visuellement. Dans d'autres exemples, comme nous le verrons ci-dessous, le canal alpha est fonctionnellement utile car les régions ombrées peuvent se chevaucher et alpha vous permet de voir les deux. Notez que le format postscript ne prend pas en charge l'alpha (il s'agit d'une limitation postscript, pas d'une limitation matplotlib), donc lorsque vous utilisez alpha, enregistrez vos figures au format PNG, PDF ou SVG.

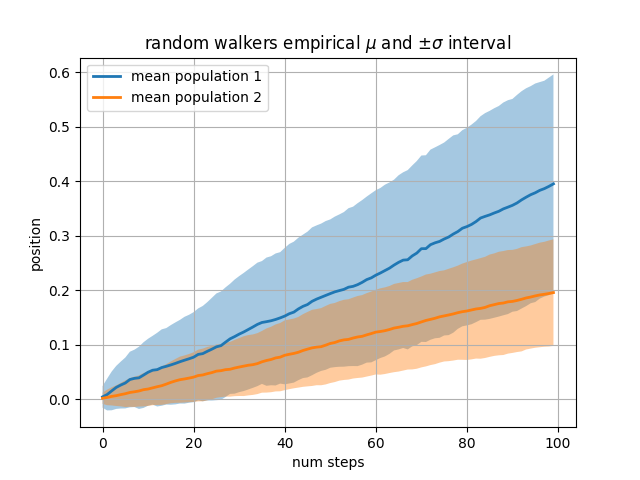
Notre exemple suivant calcule deux populations de marcheurs aléatoires avec une moyenne et un écart type différents des distributions normales à partir desquelles les pas sont tirés. Nous utilisons des régions remplies pour tracer +/- un écart type de la position moyenne de la population. Ici, le canal alpha est utile, pas seulement esthétique.

# Fixing random state for reproducibility
np.random.seed(19680801)

Nsteps, Nwalkers = 100, 250
t = np.arange(Nsteps)

# an (Nsteps x Nwalkers) array of random walk steps
S1 = 0.004 + 0.02*np.random.randn(Nsteps, Nwalkers)
S2 = 0.002 + 0.01*np.random.randn(Nsteps, Nwalkers)

# an (Nsteps x Nwalkers) array of random walker positions
X1 = S1.cumsum(axis=0)
X2 = S2.cumsum(axis=0)


# Nsteps length arrays empirical means and standard deviations of both
# populations over time
mu1 = X1.mean(axis=1)
sigma1 = X1.std(axis=1)
mu2 = X2.mean(axis=1)
sigma2 = X2.std(axis=1)

# plot it!
fig, ax = plt.subplots(1)
ax.plot(t, mu1, lw=2, label='mean population 1')
ax.plot(t, mu2, lw=2, label='mean population 2')
ax.fill_between(t, mu1+sigma1, mu1-sigma1, facecolor='C0', alpha=0.4)
ax.fill_between(t, mu2+sigma2, mu2-sigma2, facecolor='C1', alpha=0.4)
ax.set_title(r'random walkers empirical $\mu$ and $\pm \sigma$ interval')
ax.legend(loc='upper left')
ax.set_xlabel('num steps')
ax.set_ylabel('position')
ax.grid()

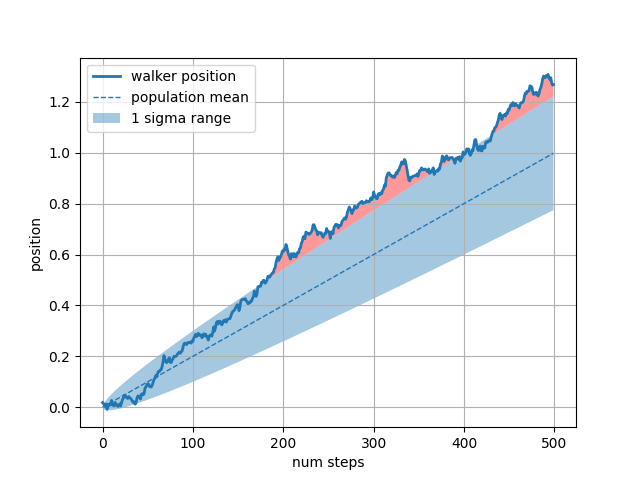
L' whereargument mot clé est très pratique pour mettre en évidence certaines régions du graphique. whereprend un masque booléen de la même longueur que les arguments x, ymin et ymax, et ne remplit que la région où le masque booléen est vrai. Dans l'exemple ci-dessous, nous simulons un marcheur aléatoire unique et calculons la moyenne analytique et l'écart type des positions de la population. La moyenne de la population est représentée par la ligne pointillée et l'écart sigma de plus/moins un par rapport à la moyenne est représenté par la région remplie. Nous utilisons le masque où pour trouver la région où le marcheur se trouve en dehors de la limite un sigma et ombrons cette région en rouge.X > upper_bound

# Fixing random state for reproducibility
np.random.seed(1)

Nsteps = 500
t = np.arange(Nsteps)

mu = 0.002
sigma = 0.01

# the steps and position
S = mu + sigma*np.random.randn(Nsteps)
X = S.cumsum()

# the 1 sigma upper and lower analytic population bounds
lower_bound = mu*t - sigma*np.sqrt(t)
upper_bound = mu*t + sigma*np.sqrt(t)

fig, ax = plt.subplots(1)
ax.plot(t, X, lw=2, label='walker position')
ax.plot(t, mu*t, lw=1, label='population mean', color='C0', ls='--')
ax.fill_between(t, lower_bound, upper_bound, facecolor='C0', alpha=0.4,
                label='1 sigma range')
ax.legend(loc='upper left')

# here we use the where argument to only fill the region where the
# walker is above the population 1 sigma boundary
ax.fill_between(t, upper_bound, X, where=X > upper_bound, fc='red', alpha=0.4)
ax.fill_between(t, lower_bound, X, where=X < lower_bound, fc='red', alpha=0.4)
ax.set_xlabel('num steps')
ax.set_ylabel('position')
ax.grid()

Une autre utilisation pratique des régions remplies consiste à mettre en évidence les étendues horizontales ou verticales d'un Axes - pour cela Matplotlib a les fonctions d'assistance axhspanet axvspan. Voir la démo axhspan .

plt.show()