Axe secondaire

Parfois, nous voulons un axe secondaire sur un tracé, par exemple pour convertir des radians en degrés sur le même tracé. Nous pouvons le faire en créant un axe enfant avec un seul axe visible via axes.Axes.secondary_xaxiset axes.Axes.secondary_yaxis. Cet axe secondaire peut avoir une échelle différente de l'axe principal en fournissant à la fois une fonction de conversion avant et une fonction de conversion inverse dans un tuple à l' argument du mot-clé functions :

import matplotlib.pyplot as plt
import numpy as np
import datetime
import matplotlib.dates as mdates
from matplotlib.ticker import AutoMinorLocator

fig, ax = plt.subplots(constrained_layout=True)
x = np.arange(0, 360, 1)
y = np.sin(2 * x * np.pi / 180)
ax.plot(x, y)
ax.set_xlabel('angle [degrees]')
ax.set_ylabel('signal')
ax.set_title('Sine wave')


def deg2rad(x):
    return x * np.pi / 180


def rad2deg(x):
    return x * 180 / np.pi


secax = ax.secondary_xaxis('top', functions=(deg2rad, rad2deg))
secax.set_xlabel('angle [rad]')
plt.show()

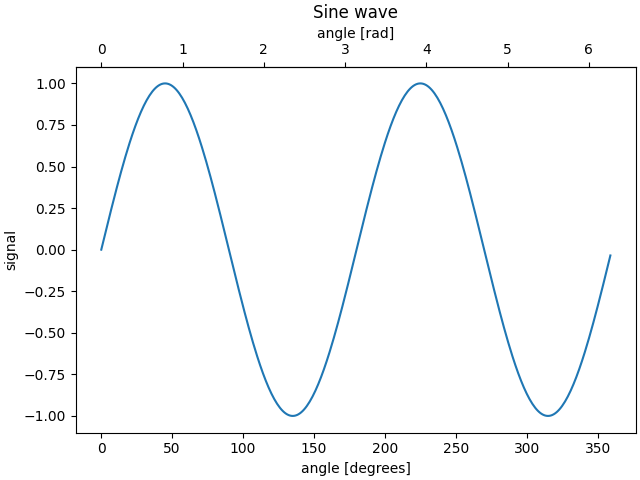
Voici le cas de la conversion du nombre d'onde en longueur d'onde dans une échelle log-log.

Noter

Dans ce cas, l'échelle x du parent est logarithmique, donc l'enfant est également rendu logarithmique.

fig, ax = plt.subplots(constrained_layout=True)
x = np.arange(0.02, 1, 0.02)
np.random.seed(19680801)
y = np.random.randn(len(x)) ** 2
ax.loglog(x, y)
ax.set_xlabel('f [Hz]')
ax.set_ylabel('PSD')
ax.set_title('Random spectrum')


def one_over(x):
    """Vectorized 1/x, treating x==0 manually"""
    x = np.array(x).astype(float)
    near_zero = np.isclose(x, 0)
    x[near_zero] = np.inf
    x[~near_zero] = 1 / x[~near_zero]
    return x


# the function "1/x" is its own inverse
inverse = one_over


secax = ax.secondary_xaxis('top', functions=(one_over, inverse))
secax.set_xlabel('period [s]')
plt.show()

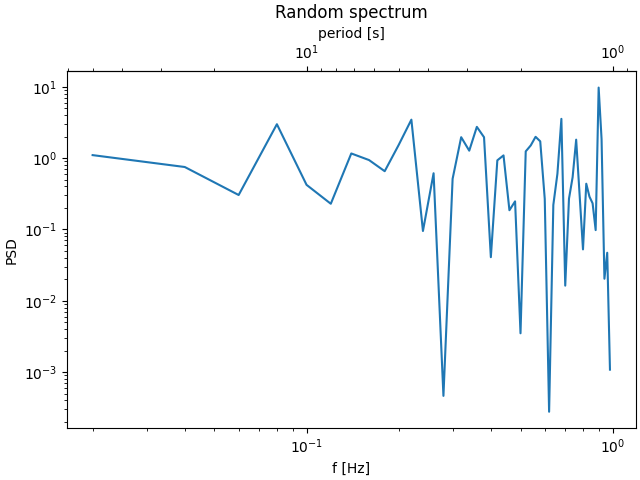
Parfois, nous voulons relier les axes dans une transformation ad hoc à partir des données et dérivée de manière empirique. Dans ce cas, nous pouvons définir les fonctions de transformation directe et inverse comme des interpolations linéaires d'un ensemble de données à l'autre.

Noter

Afin de gérer correctement les marges de données, les fonctions de mappage ( forwardet inversedans cet exemple) doivent être définies au-delà des limites nominales du tracé.

Dans le cas spécifique de l'interpolation linéaire numpy, numpy.interp, cette condition peut être arbitrairement appliquée en fournissant des arguments de mots clés facultatifs left , right de sorte que les valeurs en dehors de la plage de données soient mappées bien en dehors des limites du tracé.

fig, ax = plt.subplots(constrained_layout=True)
xdata = np.arange(1, 11, 0.4)
ydata = np.random.randn(len(xdata))
ax.plot(xdata, ydata, label='Plotted data')

xold = np.arange(0, 11, 0.2)
# fake data set relating x coordinate to another data-derived coordinate.
# xnew must be monotonic, so we sort...
xnew = np.sort(10 * np.exp(-xold / 4) + np.random.randn(len(xold)) / 3)

ax.plot(xold[3:], xnew[3:], label='Transform data')
ax.set_xlabel('X [m]')
ax.legend()


def forward(x):
    return np.interp(x, xold, xnew)


def inverse(x):
    return np.interp(x, xnew, xold)


secax = ax.secondary_xaxis('top', functions=(forward, inverse))
secax.xaxis.set_minor_locator(AutoMinorLocator())
secax.set_xlabel('$X_{other}$')

plt.show()

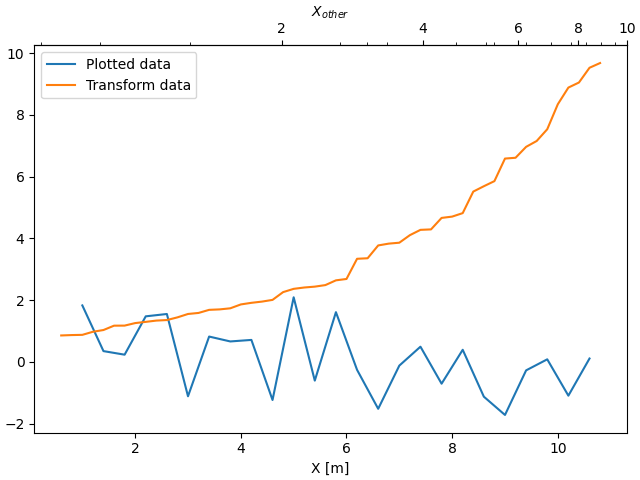
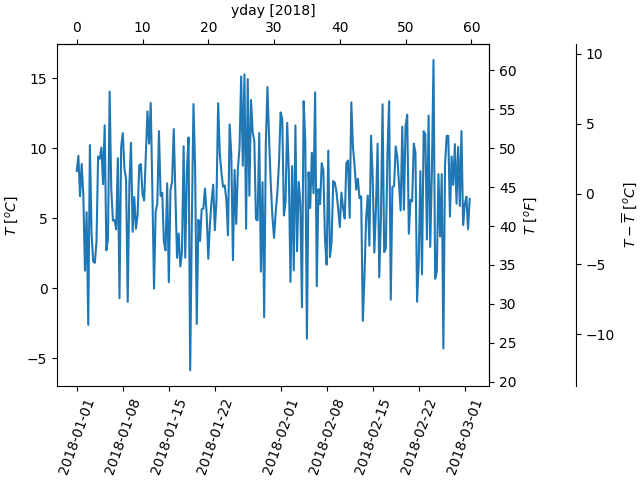
Un dernier exemple traduit np.datetime64 en jour de l'année sur l'axe des x et de Celsius en Fahrenheit sur l'axe des y. Notez l'ajout d'un troisième axe y, et qu'il peut être placé à l'aide d'un flotteur pour l'argument d'emplacement

dates = [datetime.datetime(2018, 1, 1) + datetime.timedelta(hours=k * 6)
         for k in range(240)]
temperature = np.random.randn(len(dates)) * 4 + 6.7
fig, ax = plt.subplots(constrained_layout=True)

ax.plot(dates, temperature)
ax.set_ylabel(r'$T\ [^oC]$')
plt.xticks(rotation=70)


def date2yday(x):
    """Convert matplotlib datenum to days since 2018-01-01."""
    y = x - mdates.date2num(datetime.datetime(2018, 1, 1))
    return y


def yday2date(x):
    """Return a matplotlib datenum for *x* days after 2018-01-01."""
    y = x + mdates.date2num(datetime.datetime(2018, 1, 1))
    return y


secax_x = ax.secondary_xaxis('top', functions=(date2yday, yday2date))
secax_x.set_xlabel('yday [2018]')


def celsius_to_fahrenheit(x):
    return x * 1.8 + 32


def fahrenheit_to_celsius(x):
    return (x - 32) / 1.8


secax_y = ax.secondary_yaxis(
    'right', functions=(celsius_to_fahrenheit, fahrenheit_to_celsius))
secax_y.set_ylabel(r'$T\ [^oF]$')


def celsius_to_anomaly(x):
    return (x - np.mean(temperature))


def anomaly_to_celsius(x):
    return (x + np.mean(temperature))


# use of a float for the position:
secax_y2 = ax.secondary_yaxis(
    1.2, functions=(celsius_to_anomaly, anomaly_to_celsius))
secax_y2.set_ylabel(r'$T - \overline{T}\ [^oC]$')


plt.show()

Références

L'utilisation des fonctions, méthodes, classes et modules suivants est illustrée dans cet exemple :

• matplotlib.axes.Axes.secondary_xaxis

• matplotlib.axes.Axes.secondary_yaxis