Utiliser des histogrammes pour tracer une distribution cumulative

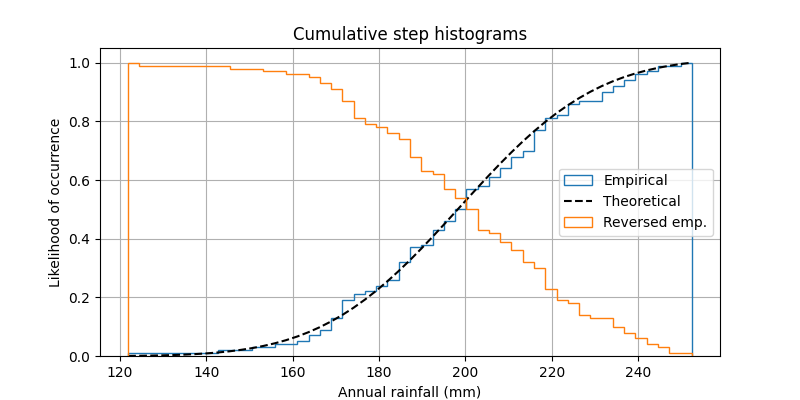
Cela montre comment tracer un histogramme cumulatif et normalisé en tant que fonction échelonnée afin de visualiser la fonction de distribution cumulative empirique (CDF) d'un échantillon. Nous montrons également le CDF théorique.

Quelques autres options de la histfonction sont démontrées. À savoir, nous utilisons le paramètre normé pour normaliser l'histogramme et quelques options différentes pour le paramètre cumulatif . Le paramètre normé prend une valeur booléenne. Lorsque True, les hauteurs des bacs sont mises à l'échelle de sorte que la surface totale de l'histogramme soit 1. L' argument du mot-clé cumulatif est un peu plus nuancé. Comme norméd , vous pouvez lui passer True ou False, mais vous pouvez aussi lui passer -1 pour inverser la distribution.

Puisque nous montrons un histogramme normalisé et cumulatif, ces courbes sont en fait les fonctions de distribution cumulatives (CDF) des échantillons. En ingénierie, les CDF empiriques sont parfois appelées courbes de "non-dépassement". En d'autres termes, vous pouvez regarder la valeur y pour une valeur x donnée pour obtenir la probabilité et l'observation de l'échantillon ne dépassant pas cette valeur x. Par exemple, la valeur de 225 sur l'axe des x correspond à environ 0,85 sur l'axe des y, il y a donc 85 % de chances qu'une observation dans l'échantillon ne dépasse pas 225 cumulative. la dernière série de cet exemple crée une courbe de "dépassement".

La sélection de différents nombres et tailles de bacs peut affecter de manière significative la forme d'un histogramme. Les documents Astropy ont une excellente section sur la façon de sélectionner ces paramètres : http://docs.astropy.org/en/stable/visualization/histogram.html

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(19680801)

mu = 200
sigma = 25
n_bins = 50
x = np.random.normal(mu, sigma, size=100)

fig, ax = plt.subplots(figsize=(8, 4))

# plot the cumulative histogram
n, bins, patches = ax.hist(x, n_bins, density=True, histtype='step',
                           cumulative=True, label='Empirical')

# Add a line showing the expected distribution.
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
     np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
y = y.cumsum()
y /= y[-1]

ax.plot(bins, y, 'k--', linewidth=1.5, label='Theoretical')

# Overlay a reversed cumulative histogram.
ax.hist(x, bins=bins, density=True, histtype='step', cumulative=-1,
        label='Reversed emp.')

# tidy up the figure
ax.grid(True)
ax.legend(loc='right')
ax.set_title('Cumulative step histograms')
ax.set_xlabel('Annual rainfall (mm)')
ax.set_ylabel('Likelihood of occurrence')

plt.show()

Références

L'utilisation des fonctions, méthodes, classes et modules suivants est illustrée dans cet exemple :

• matplotlib.axes.Axes.hist/matplotlib.pyplot.hist