Démo Asinh

Illustration de la mise à l' asinhéchelle de l'axe, qui utilise la transformation

\[a \rightarrow a_0 \sinh^{-1} (a / a_0)\]

Pour les valeurs de coordonnées proches de zéro (c'est-à-dire beaucoup plus petites que la "largeur linéaire"\(a_0\)), cela laisse les valeurs essentiellement inchangées :

\[a \rightarrow a + \mathcal{O}(a^3)\]

mais pour des valeurs plus grandes (c'est-à-dire\(|a| \gg a_0\), c'est asymptotiquement

\[a \rightarrow a_0 \, \mathrm{sgn}(a) \ln |a| + \mathcal{O}(1)\]

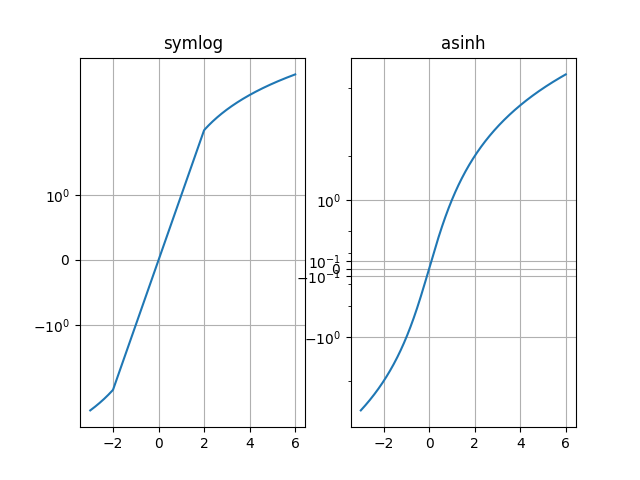
Comme pour la mise à l' symlogéchelle, cela permet de tracer des quantités qui couvrent une plage dynamique très large qui comprend à la fois des valeurs positives et négatives. Cependant, symlogimplique une transformation qui présente des discontinuités dans son gradient car elle est construite à partir de transformations linéaires et logarithmiques distinctes . La mise à l' asinhéchelle utilise une transformation qui est lisse pour toutes les valeurs (finies), qui est à la fois mathématiquement plus propre et réduit les artefacts visuels associés à une transition abrupte entre les régions linéaires et logarithmiques du tracé.

Noter

scale.AsinhScaleest expérimental et l'API peut changer.

Voir AsinhScale, SymmetricalLogScale.

import numpy as np
import matplotlib.pyplot as plt

# Prepare sample values for variations on y=x graph:
x = np.linspace(-3, 6, 500)

Comparez le comportement "symlog" et "asinh" sur l'exemple de graphique y=x, où il y a un gradient discontinu dans "symlog" près de y=2 :

fig1 = plt.figure()
ax0, ax1 = fig1.subplots(1, 2, sharex=True)

ax0.plot(x, x)
ax0.set_yscale('symlog')
ax0.grid()
ax0.set_title('symlog')

ax1.plot(x, x)
ax1.set_yscale('asinh')
ax1.grid()
ax1.set_title('asinh')

Text(0.5, 1.0, 'asinh')

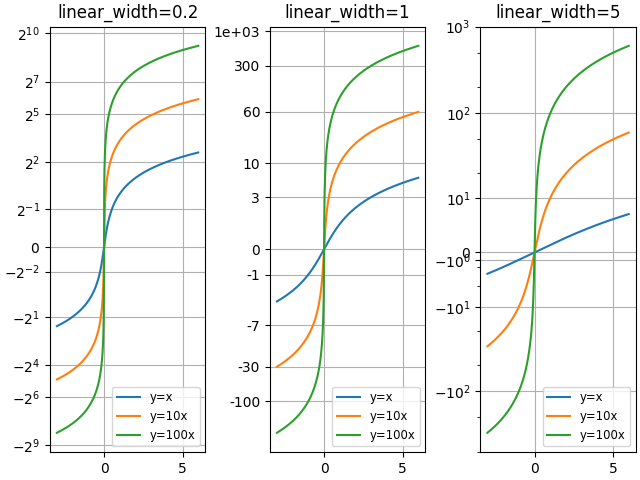
Comparez les graphiques "asinh" avec différents paramètres d'échelle "linear_width":

fig2 = plt.figure(constrained_layout=True)
axs = fig2.subplots(1, 3, sharex=True)
for ax, (a0, base) in zip(axs, ((0.2, 2), (1.0, 0), (5.0, 10))):
    ax.set_title('linear_width={:.3g}'.format(a0))
    ax.plot(x, x, label='y=x')
    ax.plot(x, 10*x, label='y=10x')
    ax.plot(x, 100*x, label='y=100x')
    ax.set_yscale('asinh', linear_width=a0, base=base)
    ax.grid()
    ax.legend(loc='best', fontsize='small')

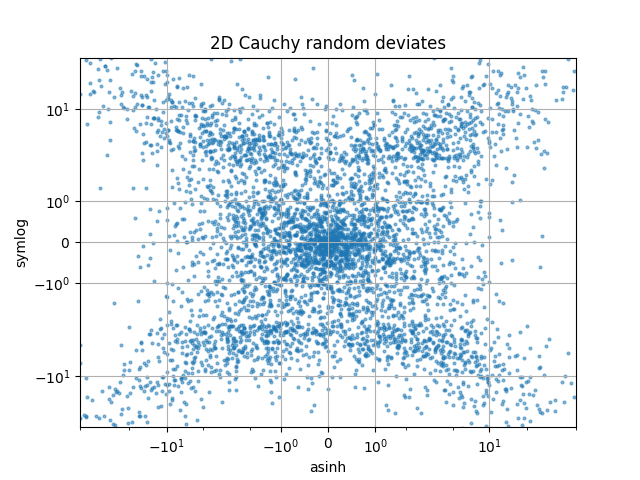
Comparez les mises à l'échelle "symlog" et "asinh" sur des nombres aléatoires 2D distribués par Cauchy, où l'on peut voir des artefacts plus subtils près de y = 2 en raison de la discontinuité du gradient dans "symlog":

fig3 = plt.figure()
ax = fig3.subplots(1, 1)
r = 3 * np.tan(np.random.uniform(-np.pi / 2.02, np.pi / 2.02,
                                 size=(5000,)))
th = np.random.uniform(0, 2*np.pi, size=r.shape)

ax.scatter(r * np.cos(th), r * np.sin(th), s=4, alpha=0.5)
ax.set_xscale('asinh')
ax.set_yscale('symlog')
ax.set_xlabel('asinh')
ax.set_ylabel('symlog')
ax.set_title('2D Cauchy random deviates')
ax.set_xlim(-50, 50)
ax.set_ylim(-50, 50)
ax.grid()

plt.show()

Références

• matplotlib.scale.AsinhScale

• matplotlib.ticker.AsinhLocator

• matplotlib.scale.SymmetricalLogScale