Noter
Cliquez ici pour télécharger l'exemple de code complet
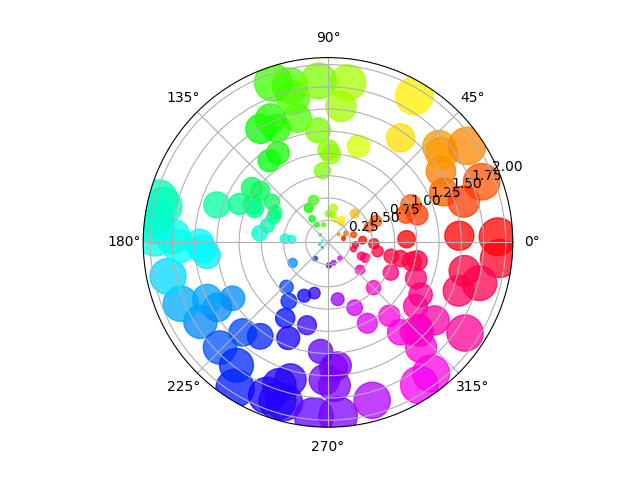
Nuage de points sur l'axe polaire #
La taille augmente radialement dans cet exemple et la couleur augmente avec l'angle (juste pour vérifier que les symboles sont correctement dispersés).
import numpy as np
import matplotlib.pyplot as plt
# Fixing random state for reproducibility
np.random.seed(19680801)
# Compute areas and colors
N = 150
r = 2 * np.random.rand(N)
theta = 2 * np.pi * np.random.rand(N)
area = 200 * r**2
colors = theta
fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)
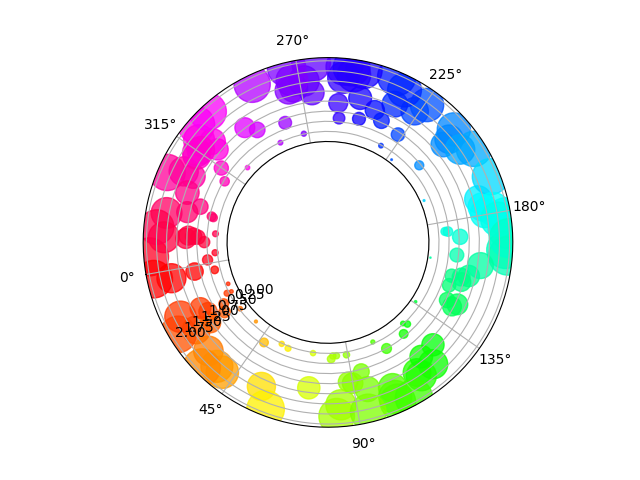
Nuage de points sur l'axe polaire, avec origine décalée #
La principale différence avec le graphique précédent est la configuration du rayon d'origine, produisant un anneau. De plus, l'emplacement thêta zéro est défini pour faire pivoter le tracé.
fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)
ax.set_rorigin(-2.5)
ax.set_theta_zero_location('W', offset=10)
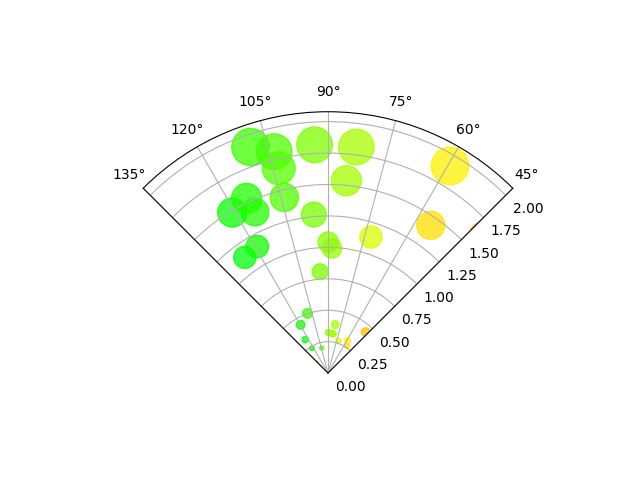
Nuage de points sur axe polaire confiné à un secteur #
La principale différence avec les graphiques précédents est la configuration des limites de début et de fin thêta, produisant un secteur au lieu d'un cercle complet.
fig = plt.figure()
ax = fig.add_subplot(projection='polar')
c = ax.scatter(theta, r, c=colors, s=area, cmap='hsv', alpha=0.75)
ax.set_thetamin(45)
ax.set_thetamax(135)
plt.show()
Références
L'utilisation des fonctions, méthodes, classes et modules suivants est illustrée dans cet exemple :
Durée totale d'exécution du script : (0 minutes 1,739 secondes)